Hadron-Hadron 충돌에서 한쪽 hadron의 quark과 다른쪽 hadron의 anti-quark이 쌍소멸하여 virtual photon 혹은 Z 보존을 만들고, 이 virtual photon과 Z 보존이 lepton 두개로 붕괴하는 process를 이야기함.

lepton 두개를 측정해서 뭔가를 하는 실험에서의 주요한 background가 된다고 한다.

더 자세히 알고 싶은 사람은 위키피디아를 참고하시라.

도선에 흐르는 전류는 Ampere단위이다. 이건 단위시간당 얼마나 많은 전하량이 흐르냐를 의미하는데, 핵물리를 하는데는 입자의 전하량이 얼마인지보다 몇개의 원자핵이 있는지가 더 중요하기 때문에 Particle Nano Ampere라는 단위를 쓸 때가 있다. 단위는 \(\text{pnA}\)라고 쓴다.

\(1\text{ A}=1\text{ C/s}\)이므로, \(1\text{ A}\)가 흐를 때 1초당 도선을 흐르는 전자의 개수는 \(\displaystyle\frac{1\text{ C}}{e}=6.242\times10^{18}\)개가 된다. 이것으로 부터 \(1\text{ A}=1\text{ pA}\)라고 두고, 가지고 있는 전하량에 관계없이 1초에 입자 \(6.242\times10^9\)개가 지나갈 때를 \(1\text{ pnA}\)로 정의한다.

\[\large 1\text{ pnA} = 6.242\times10^{9}\text{ particles/s}\]

이 글은 이수현형이 가르쳐줘 수정됐습니다.

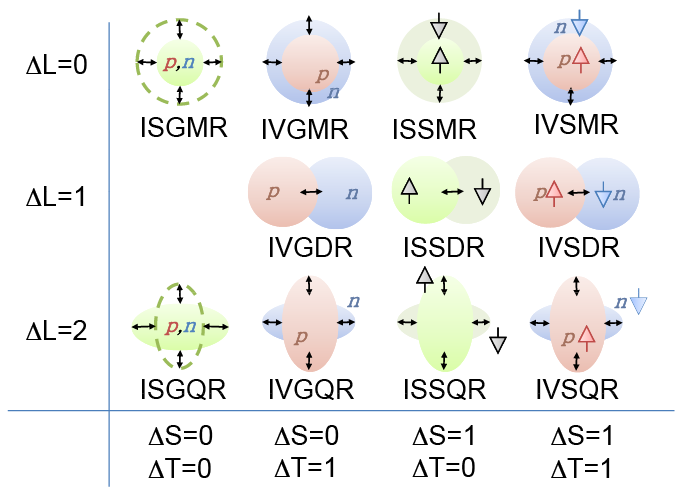
좋은 그림을 찾아서 첨부한다. 아직 의미는 모르겠다. 차차 채워넣자

\(L\): 각운동량, \(S\): 스핀 각운동량, \(T\): Isospin

• Isoscalar
  • 중성자들과 양성자들의 진동의 위상이 같을 때 (in-phase)

• Isovector
  • 중성자들과 양성자들의 진동이 위상이 180도 다를 (out-of-phase)

먼저 Gamow-Teller Transition을 읽고 오시라.

Gamow-Teller Transition을 읽어봤으면 쉽게 이해할 수 있다. \(\beta\)-붕괴에서 Fermi Transition은 반응 전·후의 강입자의 스핀은 변하지 않고, 전자와 중성미자의 스핀이 합쳐서 0이 되어 각운동량이 보존되는 반응이다. Gamow-Teller Transition과 마찬가지로 반응 전과 후의 Parity는 보존된다.

Gamow-Teller Transition, Gamow-Teller Resonance, Gamow-Teller Selection Rule 등등 여러가지 이름으로 불리는 것 같다. 어디에 쓰이느냐에 따라 조금씩 다른 것 같은데, 일단은 대강이라도 알아두자.

고등학교때 배운 \(\beta\)-붕괴를 다들 알 것이다. 이 \(\beta\)-붕괴 과정에서 각운동량 보존을 신경써줘야 하는데, Gamow-Teller Transition은 \(\beta\)-붕괴의 각운동량이 보존되는 경우들 중 한 가지이다. 예를들어 아래와 같은 반응이 있다고 해보자.

\[\large n\,\rightarrow\, p+e^-+\bar{\nu}_e\]

이 반응에서 처음 중성자의 스핀이 \(\displaystyle\frac12\)이라고 하면, Gamow-Teller Transition은 양성자의 스핀은 \(-\displaystyle\frac12\)이 되고, 전자와 전자-반중성미자의 스핀 합이 1이 되는 전이이다. 반응 전후의 Parity는 보존된다.

정리하면 강입자의 스핀은 뒤집어지고 전자와 중성미자의 스핀 합이 처음 스핀을 보존해주고, 반응 전후에 Parity가 변하지 않도록 일어나는 반응이다.

주의: Gamow-Teller Transition에서는 스핀이 정수인 경우, \(0\rightarrow0\)인 반응은 제외된다.

Spectrometer System에 이중극 자석 같은게 있으면, 이 자석이 만드는 자기장 \(\mathbf{B}\)와 하전입자 궤적의 미소길이 벡터 \(d\boldsymbol{\ell}\)의 내적을 전 궤적에 대해 적분한 값을, 그 자석의입자의 Rigidity라고 하고 식으로 적으면 아래와 같다. 이 값은 Field Integral이라고도 한다.

\[\large R=\int\mathbf{B}\cdot d\boldsymbol{\ell}\]

또, 운동량 \(p\text{ (GeV/c)}\)를 가진 전하량 \(q\)인 하전입자가 자기장이 \(\mathbf{B}\)인 곳을 지나갈 때 그리는 원궤도의 곡률반경을 \(\rho\)라고 할 때, Rigidity는 아래와 같이 정의된다.

\[\large R=B\rho=3.3356\frac{p \text{ (GeV/c)}}{q}\text{ (T}\cdot\text{m)}\]

그러니까 자석의 Rigidity가 클수록 운동량이 큰 하전입자도 잘 휠 수 있다는 말이다. 반대로 입자의 Rigidity가 클수록 이 입자는 자기장의 로렌츠힘에 영향을 덜 받는다는 말이 된다.

• 2016년 4월 22일 수정

원래 어디서 쓰던 걸 가져왔는지는 확실히 모르겠지만, 핵물리와 입자물리 실험에서 Luminosity \(\mathcal{L}\)는 다음과 같이 정의된다.

\[\large\mathcal{L}=\frac{N}{d\sigma\,dt}\]

\(N\)은 입자의 갯수, \(d\sigma\)는 입자가 통과하는 단면적이다. 따라서 Luminosity는, 단위시간당 단위면적당 몇개의 입자가 지나가는지를 나타낸다.

Luminosity를 시간에 대해 적분한 값을 Integrated Luminosity라고 한다.

\[\large\int\mathcal{L}\,dt\]

위 Luminosity식으로부터 알 수 있듯이 Integrated Luminosity는 단위면적당 입자의 갯수이다. Integrated Luminosity는 우리는 충돌실험에서 얼마만큼의 데이타를 받았는지로 사용한다. 왜그런가 질문해서 얻은 답은 아래와 같다.

실험에서 어떤 반응이 일어날 확률을 Cross section \(\sigma\)으로 나타내는데, 이는 면적의 단위를 가진 확률이다. Integrated Luminosity에 Cross section을 곱해주면 그 반응이 일어난 갯수를 주게 된다. 따라서, Integrated Luminosity가 크면 클수록 어떤 Cross section을 가진 반응의 갯수가 많아지기 때문에 데이타의 양으로 생각할 수 있다.

Cross section의 단위는 barn(\(1\,\text{b}=10^{-28}\,\text{m}^2\))을 사용한다.