나선 트랙 매개변수화(Helix Track Parametrization)에서 \(z\)축과 트랙 운동량 벡터 사이의 각도.

– 2014년 5월 20일 추가

이 매개변수화에서 보통 \(x\)축과 \(y\)축은 자기장에 수직한 방향이라 \(xy\)평면에 사영시킨 입자의 궤적은 원이고, \(z\)축은 자기장에 평행한 방향이다.

– 2014년 6월 10일 추가

나선 트랙 매개변수화(Helix Track Parametrization)에서 \(p_\mathrm{z}\)와 \(p_\mathrm{T}\)가 이루는 각도.

– 2016년 9월 27일 추가

\(r\phi\) 평면의 운동량 벡터(\(\vec{p}_\mathrm{T}\))와 3차원 운동량 벡터(\(p\))사이의 각도.

\[\tan\lambda=\frac{|\vec{p}_\mathrm{T}|}{|\vec{p}|}\]

참고문헌: algebra.pdf (http://w4.lns.cornell.edu/~ogg/Tracking)

충돌하는 두개의 원자핵을 구로 가정하고, 각각의 반지름을 \(R_1\), \(R_2\)로 놓고, Impact parameter를 \(b\)라고 할 때, 그 충돌의 Centrality는 다음과 같다.

\[\large{\text{c}\simeq\frac{\pi b^2}{\sigma_\text{inelastic}}},\qquad\text{for }b<R_1+R_2.\]

이 식은 충돌이 매우 얇은 때(Most Peripheral Collision)를 제외하고는 매우 정확하게 맞는 식이다.

기하학적인 완전비탄성 충돌의 산란단면적(Geometrical Inelastic Cross Section) \(\sigma_\text{inelastic}\)은 두 원자핵의 반지름을 더한 반지름을 가지는 원의 단면적으로,

\[\large{\sigma_\text{inelastic}=\pi(R_1+R_2)^2}\]

와 같이 정의한다.

따라서 Geometrical Centrality의 식은 아래와 같다.

\[\large{c_\text{geo}=\frac{b^2}{(R_1+R_2)^2},\qquad\text{for }b<R_1+R_2.}\]

더 자세한 설명은 상대론적 중이온 충돌에서의 중심도(Centrality)와 충격 변수(Impact parameter) 사이의 기하학적 관계를 참고.

이론물리에서 사용되는 변수들로, 입자 두개가 들어와서 두개가 나가는 산란과정에서 에너지와 운동량 그리고 각도들을 나타내는 수치값이다.

Minkowski Metric(Metric tensor)이 \(\text{diag}(1,-1,-1,-1)\)일 때, 만델스탐 변수들 \(s,t,u\)는아래와 같이 정의된다.

\[{\large\begin{align*}
s&=(p_1+p_2)^2=(p_3+p_4)^2 \\
t&=(p_1-p_3)^2=(p_2-p_4)^2 \\
u&=(p_1-p_4)^2=(p_2-p_3)^2
\end{align*}}\]

핵물리 실험에서는 주로 \(s\)를 자주 볼 수 있는데, \(\sqrt{s}\)로 나타내서 충돌에서의 질량중심 에너지를 나타낸다. 특히 핵물리 실험에서 사용하는 \(\sqrt{s_{NN}}\)는 단위 핵자당 질량중심 에너지를 나타낸다.

한가지 더 이야기하면! \(s\)는 invariant mass의 제곱과 같다.

더 자세히 알고 싶으면 위키피디아 참조.

Hadron-Hadron 충돌에서 한쪽 hadron의 quark과 다른쪽 hadron의 anti-quark이 쌍소멸하여 virtual photon 혹은 Z 보존을 만들고, 이 virtual photon과 Z 보존이 lepton 두개로 붕괴하는 process를 이야기함.

lepton 두개를 측정해서 뭔가를 하는 실험에서의 주요한 background가 된다고 한다.

더 자세히 알고 싶은 사람은 위키피디아를 참고하시라.

도선에 흐르는 전류는 Ampere단위이다. 이건 단위시간당 얼마나 많은 전하량이 흐르냐를 의미하는데, 핵물리를 하는데는 입자의 전하량이 얼마인지보다 몇개의 원자핵이 있는지가 더 중요하기 때문에 Particle Nano Ampere라는 단위를 쓸 때가 있다. 단위는 \(\text{pnA}\)라고 쓴다.

\(1\text{ A}=1\text{ C/s}\)이므로, \(1\text{ A}\)가 흐를 때 1초당 도선을 흐르는 전자의 개수는 \(\displaystyle\frac{1\text{ C}}{e}=6.242\times10^{18}\)개가 된다. 이것으로 부터 \(1\text{ A}=1\text{ pA}\)라고 두고, 가지고 있는 전하량에 관계없이 1초에 입자 \(6.242\times10^9\)개가 지나갈 때를 \(1\text{ pnA}\)로 정의한다.

\[\large 1\text{ pnA} = 6.242\times10^{9}\text{ particles/s}\]

이 글은 이수현형이 가르쳐줘 수정됐습니다.

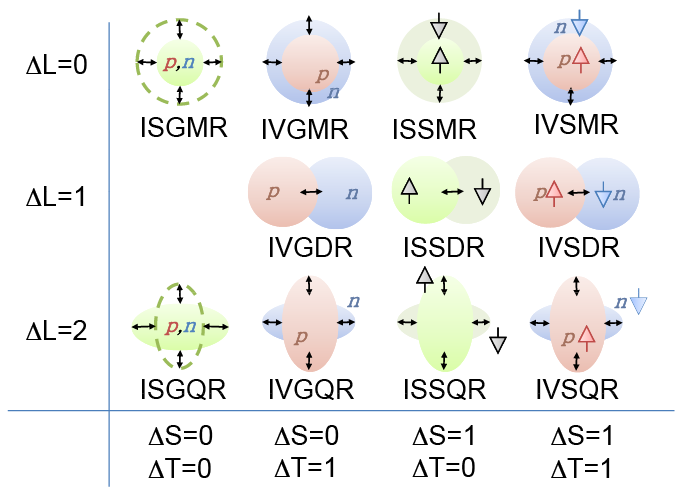
좋은 그림을 찾아서 첨부한다. 아직 의미는 모르겠다. 차차 채워넣자

\(L\): 각운동량, \(S\): 스핀 각운동량, \(T\): Isospin

• Isoscalar
  • 중성자들과 양성자들의 진동의 위상이 같을 때 (in-phase)

• Isovector
  • 중성자들과 양성자들의 진동이 위상이 180도 다를 (out-of-phase)

먼저 Gamow-Teller Transition을 읽고 오시라.

Gamow-Teller Transition을 읽어봤으면 쉽게 이해할 수 있다. \(\beta\)-붕괴에서 Fermi Transition은 반응 전·후의 강입자의 스핀은 변하지 않고, 전자와 중성미자의 스핀이 합쳐서 0이 되어 각운동량이 보존되는 반응이다. Gamow-Teller Transition과 마찬가지로 반응 전과 후의 Parity는 보존된다.